L’ElecNews n°1 : Source équilibrée et courants déséquilibrés
Introduction
Dans le cas d’un circuit déséquilibré alimenté par une source équilibrée, les tensions de phases au niveau de la charge sont très différentes de celles à la source, certaines tensions de phase au niveau de la charge peuvent même être plus élevées que celle de la source.
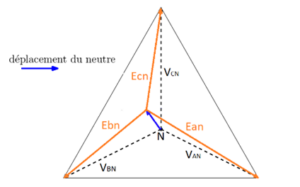
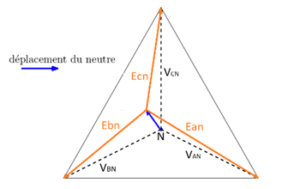
En effet, en cas de charge déséquilibrée, en raison de la circulation d’un courant dans le neutre une tension apparaît sur celui-ci et c’est cette tension qui représente le déplacement du point neutre.
Dans ce document nous allons illustrer à travers un exemple cette notion de déplacement du point neutre.
Figure 1 : Décalage du point neutre au niveau de la charge
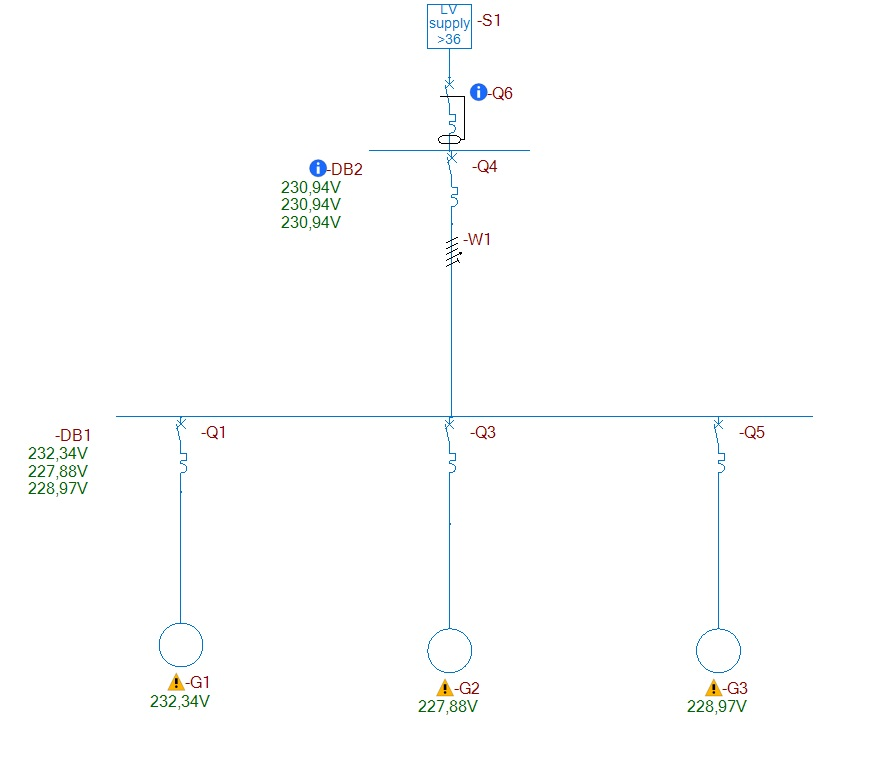
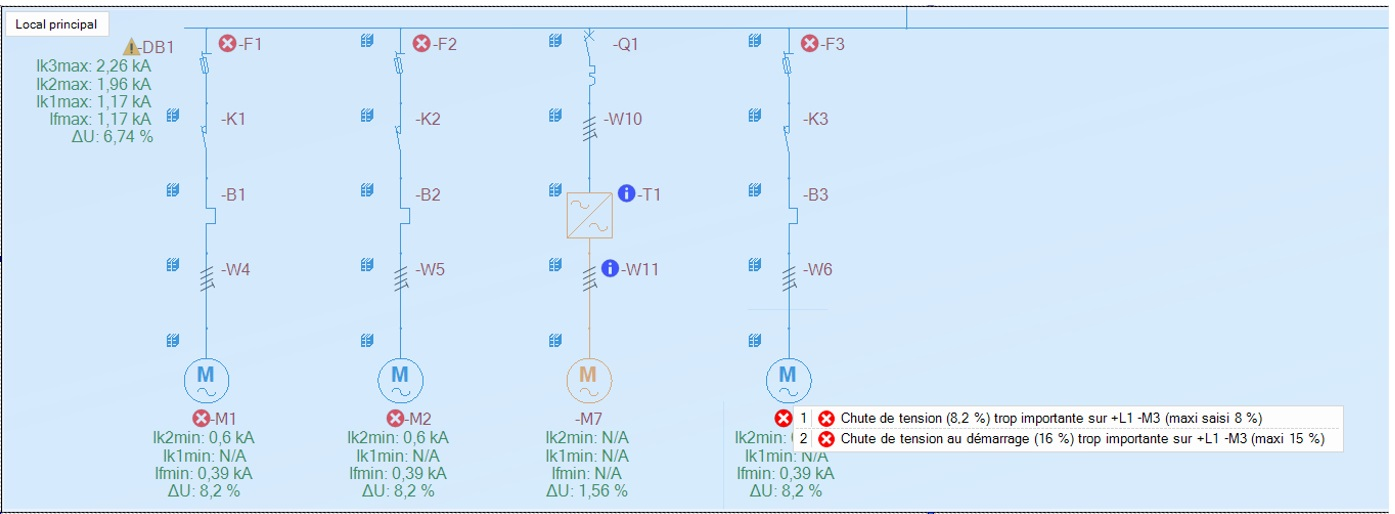
Figure 2 : Synoptique elec calc™
Reprenons les mêmes donnes d’entrée pour développer le calcul
Soit une source triphasée équilibrée alimentant une charge déséquilibrée.
Données de la souce
VAN= 230.94 ∟0° V
VBN = 230.94 ∟-120° V
VCN = 230.94 ∟+120° V
Charges
Ia = 16 ∟ -36.69° A
Ib = 50 ∟ -155.58 ° A
Ic = 30.0 ∟ 119.48° A
Zl = 0.0436 + j0.0036 ohm
ZN = 0.0436 + j0.0036 ohm
Courant dans le neutre
In = Ia + Ib + Ic
In = 16 ∟ -36.69° + 50 ∟ -155.58° + 30.0 ∟ 119.48°
In = 47.81 ∟ -175.63°
Calcul des chutes de tension dans le câble
EAa = Zl * Ia = (0.0436 + j0.0036) * 16 ∟ -36.69°
= 0.7 ∟-31.97° V
EBb =Zl * Ib = (0.0436 + j0.0036) * 50 ∟ -155.58°
= 2.18 ∟-151.45° V
ECc = Zl * Ic = (0.0436 + j0.0036) * 30.0 ∟ 119.48°
= 1.31 ∟124.2° V
ENn = Zl * In = (0.0436 + j0.0036) * 47.81 ∟ -175.63°
= 2.09 ∟-170.9° V
Tensions résiduelles à la charge
Ean = VAN – EAa– EnN = 230.94∟0° – 0.7 ∟-31.97° – 2.09 ∟-170.9° = 232.41∟0.172 ° V
Ebn = VBN – EBa– EnN = 230.94∟-120° – 2.18 ∟-151.45° – 2.09 ∟-170.9° = 227.77∟-119.3° V
Ecn = VCN – ECa– EnN = 230.94∟120° – 1.31 ∟124.2° – 2.09 ∟-170.9° =228.9 ∟119.48° V
Conclusion : On retrouve bien les tensions résiduelles correspondantes à la figure 2 . Le décalage du point neutre permet d’expliquer ce phénomène comme illustré sur la figure ci-dessous.
Figure 3 : Décalage du point neutre au niveau de la charge
Pour aller plus loin dans la réflexion, on peut s’attarder sur le calcul des puissances en composantes symétriques :
Rappelons pour commencer les fondements de cet outil mathématique. Il permet de décomposer un système triphasé déséquilibré en 3 composantes.
-
Séquence direct (d)
-
Séquence inverse (i)
-
Séquence homopolaire (o)
Puissance produite par la source
Quel que soit le déséquilibre à la charge, si la source est équilibrée, elle ne fournit que la puissance de séquence directe.
Ss = 230.94 ∟0° * 16 ∟ 36.69° * 230.94 ∟-120° * 50 ∟ 155.58 ° * 230.94 ∟+120° * 30.0 ∟ -119.48°
Ss = 21251.81∟25.31° VA (P = 19211.6 W Q = 9085.88 VAR)
La puissance apparente de séquence inverse : Ss2 = 0 (Pas de tension de séquence inverse)
La puissance apparente homopolaire: Ss0 = 0 (Pas de tension de séquence homopolaire)
Puissance de la charge
Sa = Ean * conj(Ia1) = 3718.60∟36.86° VA avec (P = 2974.92 W, Q = 2231.11 VAR )
Sb = Ebn * conj(Ia2) = 11388.59∟36.87° VA avec (P = 9110.79 W , Q = 6833.26 VAR )
Sc = Ecn * conj(Ia0) = 6866.81∟0° VA avec (P = 6866.81 W, Q = 0.11 VAR )
Sc = 21008.65∟25.56° VA avec (P = 18952.53 W, Q = 9064.49 VAR )
Pertes dans la ligne
Remarque : le courant dans le neutre est donné par la somme vectorielle des courants de phases
Pl = R*I² = 0.0436 * (16² + 50² + 30²) = 159.4 W
Ql = X*I² = 0.0036 * (16² + 50² + 30²) = 13.16 VAR
Sl = 159.94∟4.72° VA
Dans le neutre
Pn = R*I² = 0.0436 * 47.81² = 99.68 W
Qn = X*I² = 0.0036 * 47.81² = 8.23 VAR
Sn = 100 ∟4.72° VA
Au total dans le câble on a : Sln = 259.08 + i*21.39
Composantes symétriques des courants
Ia1 = 1/3 (Ia + a*Ib + a²*Ic) = 30.67∟-25.31°
Ia2 = 1/3 (Ia + a²*Ib + a*Ic) = 4.86 ∟78.25°
Ia0 = 1/3 (Ia + Ib + Ic) = -15.93∟-175.62°
Composantes symétriques des tensions le câble
El1 = 1.34 ∟-20.59°
El2 = 0.21 ∟82.97°
El0 = 0.69 ∟-170.9°
Pertes dans ligne en composantes symétriques
Sl1 = 3 * El1 * conj(Ia1) = 123.48 ∟4.72° VA avec (P = 123 W, Q = 10.16 VAR )
Sl2 = 3 * El2 * conj(Ia2) = 3.11 ∟4.72° VA avec (P = 3.1 W , Q = 0.25 VAR )
Sl0 = 3 * El0 * conj(Ia0) = 33.22 ∟4.72° VA avec (P = 33.22 W, Q = 2.74 VAR )
Comme le courant dans le neutre est par nature de séquence homopolaire on peut écrire
Sn0 = Sn = 100 ∟4.72° VA avec (P = 99.68 W, Q = 8.23 VAR )
Sn1 = 0
Sn2 = 0
On peut par là déduire les pertes totales dans le câble Sln = Sl1 + Sl2 + Sl0 + Sn0 = 259 + i*21.38
Au niveau de la charge
Tension résiduelle en composantes symétriques
Ean1 = 229.93 ∟-0.28°
Ean2 = 1.14 ∟-56.93°
Ean0 = 2.78 ∟9.09°
Puissance de la charge en composantes symétriques
Sc1 = 3 * Ean1 * conj(Ia1) = 21135.22∟25.42° VA avec (P = 19087.59 W, Q = 9075.32 VAR )
Sc2 = 3 * Ean2 * conj(Ia2) = 3.15 ∟-174.73° VA avec (P = -3.13 W , Q = -0.28 VAR )
Sc0 = 3 * Ean0 * conj(Ia0) = 133.36∟-175.27° VA avec (P = -132.36 W, Q = -10.97 VAR )
La puissance de séquence directe fournie par la source est de 19211.6 W
Les pertes dans les câbles sont de 259 W
La source fournie à la charge 19087 W de puissance de séquence directe dont 18952.32 W de puissance utile et 135.49 W (dont 3.13 W de puissance inverse et 132.36 W de puissance homopolaire) sont retournées pour compléter les pertes globales de 259 W dans la ligne.
On note que puissances de séquence inverse et de séquence homopolaire sont négatives, ce qui confirme que la charge agit comme une source pour ces deux séquences.
Résumé
Ss1 = Sc1 + Sl1 = 21135.22∟25.42° VA + 123.48 ∟4.72° VA = 21250.77 ∟25.31° VA
Sc2 = -Sl2 = -3.11 ∟4.72° VA
Sc0 = -(Sl0 + Sn0) = -(133.36 ∟-175.27° VA + 100 ∟4.72° VA) = = 233.38 ∟4.72° VA
Contrôles avec elec calc™
elec calc™ permet le calcul des différentes chutes de tension au sein de l’installation électrique selon la méthode exposée ci-dessus, ce qui garantit l’exactitude des résultats dans toutes les configurations d’installation , elec calc™ calcule :
- Chute de tension individuelle d’un composant
- Chute de tension globale depuis la source jusqu’au récepteur
- Chute de tension en régime établi
- Chute de tension au démarrage
Le calcul de la chute de tension est fait à partir des courants réels circulant dans les phases et le neutre en tenant compte des déphasages engendrés par les impédances des différents composants.
Pour un mode de fonctionnement donné, la chute de tension est calculée au nominal et au démarrage. Chaque démarrage est considéré au plus défavorable, donc avec toute l’installation alimentée.
L’utilisateur peut définir pour les récepteurs, les transformateurs, les onduleurs et les variateurs des limites spécifiques de chute de tension en régime établi, et, le cas échéant au démarrage. elec calc™ émet une alerte en cas de dépassement des seuils définis. Une alerte est également émise si les seuils définis par l’utilisateur excèdent les seuils imposés par les textes normatifs lorsqu’ils existent.